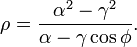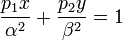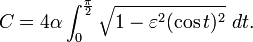Έλλειψη
Από τη Βικιπαίδεια, την ελεύθερη εγκυκλοπαίδεια
Συγκεκριμένα, ας είναι
 ,
,  δύο σημεία σε ένα ευκλείδειο επίπεδο με απόσταση 2γ μεταξύ τους και
δύο σημεία σε ένα ευκλείδειο επίπεδο με απόσταση 2γ μεταξύ τους και  ένας θετικός αριθμός. Έλλειψη ονομάζεται ο γεωμετρικός τόπος των σημείων επιπέδου των οποίων το άθροισμα των αποστάσεων από τα δύο σταθερά σημεία
ένας θετικός αριθμός. Έλλειψη ονομάζεται ο γεωμετρικός τόπος των σημείων επιπέδου των οποίων το άθροισμα των αποστάσεων από τα δύο σταθερά σημεία  είναι σταθερό και ισούται με
είναι σταθερό και ισούται με 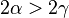 .
.Βασικές έννοιες
Τα σημεία
 ονομάζονται εστίες της έλλειψης.
ονομάζονται εστίες της έλλειψης.Το μέσο Ο του ευθύγραμμου τμήματος
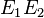 ονομάζεται κέντρο της έλλειψης. Το κέντρο της έλλειψης αποτελεί κέντρο συμμετρίας αυτής.
ονομάζεται κέντρο της έλλειψης. Το κέντρο της έλλειψης αποτελεί κέντρο συμμετρίας αυτής.Κάθε ευθύγραμμο τμήμα που έχει ως άκρα δύο διαφορετικά σημεία της έλλειψης και διέρχεται από το κέντρο αυτής ονομάζεται διάμετρος της έλλειψης.
Μία έλλειψη έχει δύο άξονες συμμετρίας, οι οποίες είναι η μικρότερη και η μεγαλύτερη διάμετρός της. Αυτές ονομάζονται μικρός και μεγάλος άξονας αντίστοιχα. O μεγάλος άξονας της έλλειψης έχει μήκος 2α, γεγονός που προκύπτει εύκολα από τον ορισμό της έλλειψης. O μικρός άξονας έχει μήκος 2β,
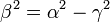 . Αυτό προκύπτει από το πυθαγόρειο θεώρημα, αν θεωρήσουμε το ορθογώνιο τρίγωνο
. Αυτό προκύπτει από το πυθαγόρειο θεώρημα, αν θεωρήσουμε το ορθογώνιο τρίγωνο 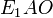 (βλ. σχήμα).
(βλ. σχήμα).Αν καλέσουμε γ την απόσταση Ε1-Ο που είναι ίση με την Ο-Ε2 και α την απόσταση ΔΟ, που είναι ίση με την ΟΒ, τότε ο λόγος γ/α = ε ονομάζεται εκκεντρότητα ή εκκεντρότης της έλλειψης.
Η εκκεντρότητα της έλλειψης,
 δηλώνει πόσο 'στενή' 'η 'πλατιά' είναι η έλλειψη.
δηλώνει πόσο 'στενή' 'η 'πλατιά' είναι η έλλειψη.- Για
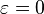 έχουμε κύκλο, ενώ για ε κοντά στο 1 μία 'μακρόστενη' έλλειψη. Συνεπώς ο κύκλος είναι έλλειψη με 0 εκκεντρότητα.
έχουμε κύκλο, ενώ για ε κοντά στο 1 μία 'μακρόστενη' έλλειψη. Συνεπώς ο κύκλος είναι έλλειψη με 0 εκκεντρότητα.
Εξισώσεις της έλλειψης
Κανονική μορφή
Μία έλλειψη θεωρείται στην κανονική της μορφή, όταν το κέντρο της είναι στο (0,0) του συστήματος συντεταγμένων και οι άξονές της είναι πάνω στους άξονές του.Σε Καρτεσιανές συντεταγμένες εκφράζεται ως:
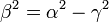 .
.Οι παραμετρικές εξισώσεις είναι:
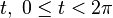 .
.Η εξίσωση της έλλειψης σε πολικές συντεταγμένες είναι:
Γενική μορφή
Έστω μία κωνική τομή Για
Για 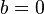 έχουμε παράλληλη μετατόπιση, ενώ για
έχουμε παράλληλη μετατόπιση, ενώ για 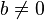 έχουμε και στροφή.
έχουμε και στροφή.Πολικές ευθείες της έλλειψης
Έστω μία έλλειψη (στην κανονική της μορφή) και ένα σημείο του επιπέδου. Η ευθεία
του επιπέδου. Η ευθεία . Το
. Το  ονομάζεται πόλος της ευθείας.
ονομάζεται πόλος της ευθείας.- Αν το
 είναι ένα σημείο της έλλειψης, τότε η πολική του είναι η εφαπτομένη της έλλειψης στο
είναι ένα σημείο της έλλειψης, τότε η πολική του είναι η εφαπτομένη της έλλειψης στο  .
.
- Έστω
 ένα εξωτερικό σημείο της έλλειψης. Τότε από αυτό διέρχονται δύο εφαπτομένες της έλλειψης. Η πολική ευθεία του
ένα εξωτερικό σημείο της έλλειψης. Τότε από αυτό διέρχονται δύο εφαπτομένες της έλλειψης. Η πολική ευθεία του  είναι η ευθεία που συνδέει τα δυο σημεία επαφής της έλλειψης με τις εφαπτομένες αυτές.
είναι η ευθεία που συνδέει τα δυο σημεία επαφής της έλλειψης με τις εφαπτομένες αυτές.
- Έστω
 ένα εσωτερικό σημείο της έλλειψης διάφορο του κέντρου της. Τότε η πολική του ευθεία δεν τέμνει την έλλειψη.
ένα εσωτερικό σημείο της έλλειψης διάφορο του κέντρου της. Τότε η πολική του ευθεία δεν τέμνει την έλλειψη.
Ιδιότητες
Ανακλαστική ιδιότητα εστιών
Έστω ένα σημείο της έλλειψης . Φέρουμε την εφαπτόμενη σε αυτό το σημείο και την κάθετη αυτής. Η κάθετη διχοτομεί την γωνία
. Φέρουμε την εφαπτόμενη σε αυτό το σημείο και την κάθετη αυτής. Η κάθετη διχοτομεί την γωνία  . Αυτό έχει την εξής συνέπεια: Αν θεωρήσουμε την εστία
. Αυτό έχει την εξής συνέπεια: Αν θεωρήσουμε την εστία  ως πηγή φωτεινής ακτινοβολίας, τότε η φωτεινή ακτίνα που εκπέμπεται από την
ως πηγή φωτεινής ακτινοβολίας, τότε η φωτεινή ακτίνα που εκπέμπεται από την  και αντανακλάται στην έλλειψη διέρχεται από την
και αντανακλάται στην έλλειψη διέρχεται από την  .
.Ορθή προβολή κύκλου
Έστω ένας κύκλος με ακτίνα σε ένα επίπεδο στον τρισδιάστατο χώρο. Θεωρούμε ένα δεύτερο επίπεδο που τέμνει το πρώτο με μία γωνία
σε ένα επίπεδο στον τρισδιάστατο χώρο. Θεωρούμε ένα δεύτερο επίπεδο που τέμνει το πρώτο με μία γωνία  και διέρχεται από το κέντρο του κύκλου. Η ορθή προβολή του κύκλου στο δεύτερο επίπεδο αποτελεί έλλειψη με άξονες μήκους
και διέρχεται από το κέντρο του κύκλου. Η ορθή προβολή του κύκλου στο δεύτερο επίπεδο αποτελεί έλλειψη με άξονες μήκους 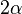 και
και 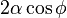 .
.Κάθε έλλειψη μπορεί να εκφραστεί ως ορθή προβολή κύκλου.
Συζυγείς διάμετροι
Έστω μία έλλειψη και ένας κύκλος του οποίου η ορθή προβολή είναι η έλλειψη αυτή. Δύο διάμετροι της έλλειψης ονομάζονται συζυγείς, όταν αποτελούν ορθή προβολή δύο κάθετων διαμέτρων του κύκλου.Μία διάμετρος έλλειψης διέρχεται από τα μέσα όλων των χορδών που είναι παράλληλες με τη συζυγή της.