Ο Γιόχαν Καρλ Φρίντριχ Γκάους (Johann Carl Friedrich Gauss, στη γερμανική συνήθως γράφεται ως Gauß) (30 Απριλίου 1777 – 23 Φεβρουαρίου 1855) ήταν Γερμανός μαθηματικός που συνεισέφερε σε πολλά ερευνητικά πεδία της επιστήμης του, όπως η θεωρία αριθμών, η στατιστική, η μαθηματική ανάλυση, η διαφορική γεωμετρία, αλλά και συναφών επιστημών, όπως η γεωδαισία, η αστρονομία και η φυσική (ηλεκτροστατική, οπτική, γεωμαγνητισμός). Αποκλήθηκε «ο πρίγκηψ των μαθηματικών» και ο «μεγαλύτερος μαθηματικός μετά τον Αρχιμήδη και τον Ευκλείδη». Ο Γκάους υπήρξε ίσως ο σημαντικότερος Γερμανός μαθηματικός όλων των εποχών και ένας από τους δύο ή τρεις σπουδαιότερους των νεότερων χρόνων (μετά την αρχαιότητα) (Waldo Dunnington: "The Sesquicentennial of the Birth of Gauss", Scientific Monthly, τόμος 24, σ. 402-414).
Ο Γκάους ήταν αυτό που αποκαλείται «παιδί-θαύμα» και υπάρχουν αρκετές ιστορίες για τις εκπληκτικές του ικανότητες ως νηπίου, ενώ οι πρώτες μεγάλες μαθηματικές ανακαλύψεις του χρονολογούνται από την εφηβεία του. Σε ηλικία 21 ετών είχε ολοκληρώσει το κύριο έργο του στα καθαρά μαθηματικά, το Disquisitiones Arithmeticae, (= «Αριθμητικές Έρευνες», 1798, εκδόθηκε το 1801). Αυτό το έργο διαδραμάτισε θεμελιώδη ρόλο στην εδραίωση της θεωρίας αριθμών ως αυτοδύναμου κλάδου των μαθηματικών και τη σημάδεψε μέχρι τις μέρες μας.
Τα πρώτα χρόνια
Η γνωστότερη ίσως ιστορία αφορά την απόπειρα του δασκάλου του στο δημοτικό, του J.G. Büttner, να απασχολήσει τους μαθητές του σε μια κενή ώρα βάζοντάς τους να προσθέσουν όλους τους ακεραίους από το 1 ως το 100. Ο μικρός Γκάους βρήκε το σωστό άθροισμα σε λιγότερο από 1 λεπτό, εκπλήσσοντας τόσο τον δάσκαλο όσο και τον βοηθό του Martin Bartels. Ο Γκάους αντιλήφθηκε ότι η πρόσθεση κατά ζεύγη από τις δύο άκρες αυτής της σειράς των αριθμών έδινε πάντα το ίδιο άθροισμα: 1 + 100 = 101, 2 + 99 = 101, 3 + 98 = 101, κ.ο.κ., οπότε για ένα ολικό άθροισμα 50 × 101 = 5050 (βλ. αριθμητική σειρά). Ο J. Rotman πάντως γράφει στο βιβλίο του A first course in Abstract Algebra ότι πιστεύει πως αυτό το περιστατικό δεν συνέβη ποτέ.
Ο πατέρας του Γκάους τον προέτρεπε να ακολουθήσει το επάγγελμά του και να γίνει χτίστης ξύλινων σπιτιών. Δεν συμφωνούσε να μάθει ο Καρλ μαθηματικά και επιστήμες. Σε αυτή την προσπάθεια, ο Γκάους είχε κυρίως την υποστήριξη της μητέρας του και μετά του Δούκα του Brunswick-Lüneburg, που του έδωσε μια υποτροφία για να σπουδάσει στο Collegium Carolinum (το σημερινό Πολυτεχνείο του Μπράουνσβαϊγκ), όπως και έγινε, από το 1792 ως το 1795. Στη συνέχεια, σπούδασε στο Πανεπιστήμιο του Γκέτινγκεν από το 1795 ως το 1798. Κατά τη διάρκεια των σπουδών του, ο Γκάους πέτυχε να ανακαλύψει εκ νέου και από μόνος του πολλά ήδη γνωστά σημαντικά θεωρήματα. Η πρώτη του νέα ανακάλυψη ήταν το 1796, όταν απέδειξε ότι οποιοδήποτε κανονικό πολύγωνο του οποίου ο αριθμός πλευρών είναι πρώτος αριθμός Φερμά (και, συνεπώς, και όλα τα πολύγωνα με αριθμό πλευρών γινόμενο ξεχωριστών πρώτων αριθμών Φερμά και μιας δυνάμεως του 2) μπορεί να κατασκευασθεί με κανόνα και διαβήτη. Αυτή ήταν μια σημαντική ανακάλυψη σε ένα βασικό πεδίο των μαθηματικών. Τα προβλήματα «κατασκευής» απασχολούσαν τους μαθηματικούς από την Αρχαία Ελλάδα και η ανακάλυψη αυτή τελικώς οδήγησε τον Γκάους να επιλέξει μια σταδιοδρομία στα μαθηματικά αντί για τη φιλολογία. Ευχαριστήθηκε τόσο από αυτή την ανακάλυψη, ώστε ζήτησε να χαραχθεί πάνω στον τάφο του ένα κανονικό δεκαεπτάγωνο. Ο τεχνίτης αρνήθηκε, δηλώνοντας ότι η δύσκολη αυτή κατασκευή θα φαινόταν σχεδόν σαν ένας κύκλος.
». Την 1η Oκτωβρίου δημοσίευσε ένα αποτέλεσμα για τον αριθμό των λύσεων πολυωνύμων με συντελεστές σε πεπερασμένα πεδία (αυτό οδήγησε τελικώς στις Εικασίες του Weil 150 χρόνια μετά).Τα ώριμα χρόνια
Στη διατριβή του με τίτλο «Μία νέα απόδειξη ότι κάθε ρητή συνάρτηση μιας μεταβλητής μπορεί να αναλυθεί σε πραγματικούς παράγοντες του πρώτου ή του δεύτερου βαθμού» (1799, υπό την επίβλεψη του Γιόχαν Φρίντριχ Πφαφ) ο Γκάους έδωσε μία απόδειξη του θεμελιώδους θεωρήματος της άλγεβρας. Το σημαντικό αυτό θεώρημα δηλώνει ότι κάθε πολυώνυμο πρέπει να έχει τουλάχιστον μία ρίζα στο σύνολο των μιγαδικών αριθμών. Πριν από τον Γκάους είχαν προσπαθήσει και άλλοι μαθηματικοί να αποδείξουν αυτό το θεώρημα, όπως ο Ζαν λε Ροντ ντ' Αλαμπέρ. Η διατριβή του Γκάους περιείχε και μία κριτική της αποδείξεως του ντ' Αλαμπέρ, αλλά η ίδια η δική του απόδειξη δεν έγινε δεκτή εξαιτίας της υπονοούμενης χρήσεως του θεωρήματος καμπυλών του Jordan. Στο υπόλοιπο της ζωής του ο Γκάους παρήγαγε τρεις ακόμα αποδείξεις του: η τελευταία, το 1849, θεωρείται γενικώς αυστηρή με τα σημερινά πρότυπα. Οι προσπάθειές του ξεκαθάρισαν την έννοια του μιγαδικού αριθμού (στην τρίτη απόδειξη, το 1816, είχε κάνει χρήση μιγαδικών ολοκληρωμάτων).Το 1801 ο Ιταλός αστρονόμος Τζιουζέπε Πιάτσι ανακάλυψε τον πρώτο αστεροειδή, τη Δήμητρα, αλλά μπόρεσε να την παρατηρήσει επί λίγες μόνο νύχτες. Ο Γκάους προέβλεψε σωστά τη θέση στην οποία θα βρισκόταν στο μέλλον, όπου και ξαναπαρατηρήθηκε από τον Φραντς φον Ζαχ στις 3 Δεκεμβρίου 1801 και από τον Χάινριχ Όλμπερς μία μέρα αργότερα. Ο Ζαχ σημείωσε ότι «χωρίς την ευφυή εργασία και τους υπολογισμούς του δόκτορα Γκάους ίσως να μην είχαμε ξαναβρεί τη Δήμητρα». Ο Γκάους, που μέχρι τότε στηριζόταν οικονομικά από τον δούκα, αμφέβαλλε για τη σταθερότητα αυτής της υποστήριξης, καθώς δεν πίστευε ότι τα καθαρά μαθηματικά ήταν αρκετά σημαντικά ώστε να αξίζουν υποστήριξη, οπότε μετά την αστρονομική του επιτυχία επεδίωξε μία θέση στην αστρονομία: Το 1807 διορίσθηκε καθηγητής της αστρονομίας και διευθυντής του αστεροσκοπείου στο Γκέτινγκεν, μία θέση που διατήρησε για το υπόλοιπο της ζωής του.
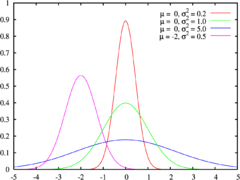
Η ανακάλυψη της Δήμητρας οδήγησε τον Γκάους να επεξεργασθεί μία θεωρία για τις κινήσεις μικρών σωμάτων που διαταράσσονται από μεγάλους πλανήτες, η οποία τελικώς εκδόθηκε το 1809 με τον τίτλο Theoria motus corporum coelestium in sectionibus conicis solem ambientum («Θεωρία της κινήσεως των ουρανίων σωμάτων που κινούνται σε κωνικές τομές περί τον Ήλιο»). Αυτή η θεωρία, για την οποία εργάσθηκε έντονα επί τρεις μήνες σε ηλικία 23 ετών, οδήγησε στην ορθή πρόβλεψη της θέσεως της Δήμητρας με ακρίβεια μισής μοίρας. Η εργασία αυτή, που επανεκδόθηκε λίγα χρόνια μετά ως «Θεωρία της ουρανίου κινήσεως», παραμένει ένας θεμέλιος λίθος των αστρονομικών υπολογισμών. Περιείχε μια πραγμάτευση της Μεθόδου των ελάχιστων τετραγώνων, μια μέθοδο που χρησιμοποιείται σε όλες τις επιστήμες μέχρι σήμερα για να ελαχιστοποιήσει την επίδραση των σφαλμάτων στις μετρήσεις. Ο Γκάους μπόρεσε να αποδείξει τη μέθοδο το 1809 υπό την παραδοχή σφαλμάτων που ακολουθούν την κανονική κατανομή (βλ. Θεώρημα Gauss-Markov, γκαουσιανή). Η μέθοδος είχε περιγραφεί το 1805 από τον Αντριάν-Μαρί Λεζάντρ, αλλά ο Γκάους ισχυρίσθηκε ότι ο ίδιος τη χρησιμοποιούσε από το 1795.
Το 1818 ο Γκάους, βρίσκοντας μια πρακτική χρήση των υπολογιστικών του ικανοτήτων, έκανε μια γεωδαιτική επισκόπηση του κρατιδίου του Ανόβερου, ενώνοντάς το με προηγηθείσες δανέζικες επισκοπήσεις. Για αυτή την εργασία ο Γκάους εφηύρε το όργανο ηλιοτρόπιο, μια διάταξη που με ένα κάτοπτρο ανακλά το ηλιακό φως σε μεγάλες αποστάσεις για την ακριβή μέτρηση θέσεων.
Ο Γκάους επίσης ισχυρίσθηκε ότι είχε ανακαλύψει τη δυνατότητα για μη ευκλείδειες γεωμετρίες, αλλά δεν τη δημοσίευσε ποτέ. Αυτή η ανακάλυψη ήταν ένας σταθμός στα μαθηματικά, καθώς απελευθέρωσε τους μαθηματικούς από τη λανθασμένη πεποίθηση ότι τα αξιώματα του Ευκλείδη ήταν ο μόνος τρόπος για να είναι η γεωμετρία αυτοσυνεπής. Η έρευνα στις μη ευκλείδειες γεωμετρίες απετέλεσε, μεταξύ άλλων, το υπόβαθρο για τη γενική θεωρία της σχετικότητας του Αϊνστάιν, που περιγράφει τον χώρο του Σύμπαντος ως μη ευκλείδειο. Ο φίλος του Φάρκας Μπολυαί, με τον οποίο ο Γκάους είχε ορκισθεί «αδελφοσύνη και ειλικρίνεια» ως φοιτητής, είχε προσπαθήσει μάταια επί πολλά έτη να αποδείξει το αξίωμα των παράλληλων ευθειών από τα υπόλοιπα γεωμετρικά αξιώματα του Ευκλείδη. Ο γιος του Φάρκας, ο Γιάνος Μπολυαί, κατέληξε στη μη ευκλείδεια γεωμετρία το 1829, ενώ η εργασία του δημοσιεύθηκε το 1832. Αφού τη διάβασε, ο Γκάους έγραψε στον Φάρκας Μπολυαί: «Το να την εξυμνήσω θα ήταν ισοδύναμο με το να εξυμνήσω τον εαυτό μου. Γιατί ολόκληρο το περιεχόμενό της ... συμπίπτει σχεδόν ακριβώς με τις δικές μου σκέψεις, που απασχολούν το μυαλό μου τα τελευταία 30 ή 35 χρόνια.» Αυτός ο αναπόδεικτος ισχυρισμός έθεσε σε δοκιμασία τις σχέσεις του με τον Γιάνος Μπολυαί (που νόμιζε ότι ο Γκάους του «έκλεβε» την ιδέα), αλλά σήμερα θεωρείται γενικά ότι ήταν αληθής: Επιστολές του Γκάους πριν το 1829 τον εμφανίζουν να συζητά το πρόβλημα των παράλληλων ευθειών, π.χ. το 1817 ο Γκάους εξέφραζε ιδιωτικά τη βαθιά του απογοήτευση από την ευκλείδεια γεωμετρία. Σε μια προφητική του επιστολή προς το φίλο του αστρονόμο Όλμπερς, δήλωνε καθαρά ότι η ευκλείδεια γεωμετρία είναι μαθηματικώς ατελής. Ο Dunnington στο έργο του «Γκάους, Τιτάν της Επιστήμης», δείχνει με αρκετή επιτυχία ότι ο Γκάους κατείχε πλήρως τη μη ευκλείδεια γεωμετρία πολύ πριν αυτή δημοσιευθεί από τον Γιάνος, αλλά αρνήθηκε να την κοινοποιήσει φοβούμενος αντιδράσεις από τους συντηρητικούς μαθηματικούς: το 1829, ο Γκάους εξομολογήθηκε στον φοιτητή και φίλο του Φρίντριχ Βίλχελμ Μπέσελ ότι δεν θα δημοσίευε ποτέ τη δουλειά του πάνω στις μη ευκλείδιες γεωμετρίες γιατί φοβόταν τη διαμάχη που θα προκαλούσε ανάμεσα στους «Βοιωτούς». Ο μαθηματικός Morris Kline έγραψε: «[ο Γκάους] έλεγε σε ένα γράμμα στον Bessel της 27ης Ιανουαρίου 1829, ότι πιθανώς δεν θα δημοσίευε ποτέ τα ευρήματά του στο αντικείμενο αυτό, επειδή φοβόταν τη γελοιοποίηση, ή όπως το έθετε, φοβόταν την κατακραυγή των Βοιωτών, μια μεταφορική αναφορά σε μια καθυστερημένη ελληνική φυλή» (Mathematics and the Physical World, Νέα Υόρκη: Crowell, 1959, σελ. 449).
Τα ύστερα χρόνια και ο θάνατος
Το 1831 ο Γκάους άρχισε μια προσοδοφόρα συνεργασία με τον καθηγητή της φυσικής Βίλχελμ Βέμπερ, που οδήγησε σε νέες γνώσεις στο πεδίο του μαγνητισμού (όπως η εξεύρεση μιας σχέσεως για τη μονάδα της εντάσεως του μαγνητικού πεδίου με τη μάζα, το μήκος και τον χρόνο) και την ανακάλυψη των λεγόμενων «νόμων του Κίρχοφ» στον ηλεκτρισμό. Οι Γκάους και Βέμπερ κατασκεύασαν τον πρώτο ηλεκτρικό τηλέγραφο το 1833, η γραμμή του οποίου συνέδεε το αστεροσκοπείο με το Ινστιτούτο Φυσικής στο Γκέτινγκεν. Ο Γκάους παρήγγειλε ένα γεωμαγνητικό παρατηρητήριο να κτισθεί στον κήπο του αστεροσκοπείου και ίδρυσε με τον Βέμπερ τη «Μαγνητική Λέσχη» (magnetischer Verein), για την υποστήριξη μετρήσεων του μαγνητικού πεδίου της Γης σε πολλές περιοχές του κόσμου. Ο Γκάους ανέπτυξε μέθοδο για τη μέτρηση της οριζόντιας συνιστώσας της μαγνητικής επαγωγής του γεωμαγνητικού πεδίου, που χρησιμοποιήθηκε μέχρι και το 1970 περίπου, ενώ επεξεργάσθηκε τη μαθηματική θεωρία για τον διαχωρισμό του εσωτερικού πυρήνα της Γης, του φλοιού και των εξωτερικών μαγνητοσφαιρικών πηγών του μαγνητικού πεδίου της Γης.Ο Γκάους απεβίωσε στο Γκέτινγκεν σε ηλικία 78 ετών και η σορός του αναπαύεται στο κοιμητήριο Albanifriedhof εκεί. Μόνο δύο άνθρωποι εκφώνησαν επικήδειο λόγο στην κηδεία του, ο γαμπρός του Heinrich Ewald και ο καλός του φίλος και βιογράφος Wolfgang Sartorius von Waltershausen. Ο εγκέφαλος του Γκάους συντηρήθηκε ξεχωριστά και μελετήθηκε από τον Ρούντολφ Βάγκνερ, που βρήκε τη μάζα του ίση με 1.492 γραμμάρια και την επιφάνειά του 219.588 mm2 με εκτεταμένες και πολύπλοκες έλικες (Dunnington, 1927).
Οικογένεια
Η προσωπική ζωή του Γκάους επισκιάσθηκε από τον πρόωρο θάνατο της πρώτης του συζύγου, της Γιοχάνα Όστχοφ (1780-1809), τον οποίο ακολούθησε σύντομα ο θάνατος ενός παιδιού, του Λουί. Ο Γκάους βυθίσθηκε σε κατάθλιψη, από την οποία δεν συνήλθε ποτέ τελείως, παρότι ξαναπαντρεύτηκε με μια φίλη της Γιοχάνα, τη Φριντερίκα Βιλελμίνε Βάλντεκ (Μίνα), η οποία δυστυχώς ήταν χρόνια άρρωστη. Μόλις και η δεύτερη σύζυγός του πέθανε, το 1831, μία από τις κόρες του Γκάους, η Τερέζα, ανέλαβε το σπιτικό και φρόντιζε τον μαθηματικό μέχρι τον θάνατό του. Η μητέρα του ζούσε στο ίδιο σπίτι από το 1817 ως τον θάνατό της το 1839.Ο Γκάους και η Γιοχάνα είχαν τρία παιδιά, τον Γιόζεφ (1806-1873), τη Βιλελμίνα (1808-1846) και τον Λουί (1809-1810). Με τη Μίνα, ο Γκάους απέκτησε άλλα τρία: τον Εουγκένε (1811-1896), τον Βίλχελμ (1813-1879) και την Τερέζα(1816-1864). Από όλα τα παιδιά η Βιλελμίνα λεγόταν ότι πλησίαζε περισσότερο στο ταλέντο του, αλλά πέθανε νέα. Ο Εουγκένε μετανάστευσε στις ΗΠΑ περί το 1832 αφού μάλωσε με τον πατέρα του και εγκαταστάθηκε τελικά στο Σαιντ Τσαρλς του Μισούρι. Εκεί εγκαταστάθηκε αργότερα και ο Βίλχελμ, που πρόκοψε ως βιοτέχνης-υποδηματοποιός. Ας σημειωθεί ότι ο ίδιος ο Γκάους δεν επιθυμούσε τα παιδιά του να ασχοληθούν με τα μαθηματικά ή τις επιστήμες φοβούμενος «μη λερώσουν την καλή φήμη που δημιούργησε ο ίδιος για το οικογενειακό όνομα στους τομείς αυτούς», όπως αναφέρεται σε γράμμα από τον εγγονό του Robert Gauss προς τον Φέλιξ Κλάιν στις 3 Σεπτεμβρίου 1912.
Προσωπικότητα
Ο Γκάους ήταν τελειομανής και σκληρά εργαζόμενος. Σύμφωνα με τον Ισαάκ Ασίμοφ, κάποτε τον διέκοψαν στη μέση ενός προβλήματος και του είπαν ότι η σύζυγός του πέθαινε, οπότε λέγεται ότι απάντησε «Πες της να περιμένει μια στιγμή να τελειώσω» (Asimov: Biographical Encyclopedia of Science and Technology. Τhe Lives and Achievements of 1195 Great Scientists from Ancient Times to the Present, Chronologically Arranged. Νέα Υόρκη 1972: Doubleday).Αρνιόταν να δημοσιεύσει εργασίες που δεν θεωρούσε πλήρεις και πέρα από κάθε κριτική: το προσωπικό του σύνθημα ήταν pauca sed matura (= «λίγα, αλλά ώριμα»). Η εξέταση των προσωπικών του ημερολογίων αποκαλύπτει ότι στην πραγματικότητα είχε ανακαλύψει αρκετές σημαντικές μαθηματικές συλλήψεις χρόνια ή δεκαετίες πριν αυτές πρωτοδημοσιευθούν από άλλους μαθηματικούς. Ο ιστορικός των μαθηματικών Έρικ Τεμπλ Μπελ εκτιμά ότι αν ο Γκάους είχε γνωστοποιήσει όλες του τις ανακαλύψεις, τα μαθηματικά θα είχαν προχωρήσει κατά 50 χρόνια (Bell: Men of Mathematics: The Lives and Achievements of the Great Mathematicians from Zeno to Poincaré, Νέα Υόρκη 1986: Simon and Schuster, σελ. 218-269).
Η κριτική που ασκείται στον Γκάους είναι ότι δεν υποστήριζε τους νεότερους μαθηματικούς που τον ακολούθησαν. Σπανίως συνεργαζόταν με άλλους μαθηματικούς και πολλοί τον θεωρούσαν επιφυλακτικό και αυστηρό. Παρότι δίδαξε φοιτητές, ο Γκάους ήταν γνωστό ότι αντιπαθούσε τη διδασκαλία. Λέγεται ότι παρακολούθησε μόνο ένα επιστημονικό συνέδριο σε ολόκληρη τη ζωή του, στο Βερολίνο το 1828. Ωστόσο, αρκετοί από τους φοιτητές του εξελίχθηκαν σε επιφανείς μαθηματικούς, όπως οι Ρίχαρντ Ντέντεκιντ, Μπέρναρντ Ρίμαν και Φρίντριχ Βίλχελμ Μπέσελ.
Ο Γκάους συνήθως αρνιόταν να παρουσιάσει τη διαίσθηση πίσω από τις συχνά κομψότατες αποδείξεις του. Προτιμούσε να εξαφανίζει όλα τα ίχνη του πώς τις είχε σκεφθεί. Ο ίδιος εξηγεί στις Disquisitiones Arithmeticae ότι όλη η ανάλυση (με την έννοια του δρόμου που έπαιρνε κάποιος για να φθάσει στη λύση ενός προβλήματος) πρέπει να παραλείπεται για χάρη συντομίας.
Ο Γκάους είχε βαθιά θρησκευτική πίστη και ήταν και συντηρητικός πολιτικά: υποστήριζε τη μοναρχία και αντιπαθούσε τον Ναπολέοντα, που τον έβλεπε ως γέννημα της επαναστάσεως.
Ονομάσθηκαν προς τιμή του
- Η μονάδα του συστήματος cgs για τη μαγνητική επαγωγή (1 gauss).
- Το επίπεδο Γκάους, πάνω στο οποίο βρίσκουν τη θέση τους οι μιγαδικοί αριθμοί.
- Ο Νόμος του Γκάους στον ηλεκτρομαγνητισμό (μία από τις 4 εξισώσεις του Μάξγουελ)
- Ο αστεροειδής 1001 Γκαούσια (1001 Gaussia), που ανακαλύφθηκε το 1923.
- Ο κρατήρας Γκάους στη Σελήνη.
- Το πλοίο της πρώτης γερμανικής εξερευνητικής αποστολής στην Ανταρκτική.
- Το Γκάουσμπεργκ (Gaussberg = «Βουνό του Γκάους»), ένα εσβεσμένο ηφαίστειο που ανακαλύφθηκε από την παραπάνω εξερευνητική αποστολή.
- Ο «Πύργος Γκάους», ένας πύργος παρατηρήσεων.
- Στα γυμνάσια του Καναδά ένας ετήσιος εθνικός διαγωνισμός Μαθηματικών που διοργανώνεται από το «Κέντρο για την Εκπαίδευση στα Μαθηματικά και την Υπολογιστική» φέρει επίσης το όνομα του Γκάους.
- Το Gauss Haus, ένα κέντρο NMR στο Πανεπιστήμιο της Γιούτα.
- Από το 1989 ως την κατάργηση του νομίσματος το 2000, η προσωπογραφία του Γκάους και μια γκαουσιανή καμπύλη μαζί με κάποια κτήρια του Γκέτινγκεν απεικονίζονταν στο γερμανικό χαρτονόμισμα των 10 μάρκων. Στην άλλη πλευρά του ίδιου χαρτονομίσματος απεικονιζόταν το ηλιοτρόπιο και μια προσέγγιση τριγωνισμού για το Ανόβερο. Επίσης, η Γερμανία έχει εκδώσει τρία γραμματόσημα προς τιμή του Γκάους, το 1955 για τα 100 χρόνια από τον θάνατό του και δύο το 1977 για τα 200 από τη γέννησή του.
